Bayesian Inverse Methods for Ice Sheet Model Calibration and Reconstruction

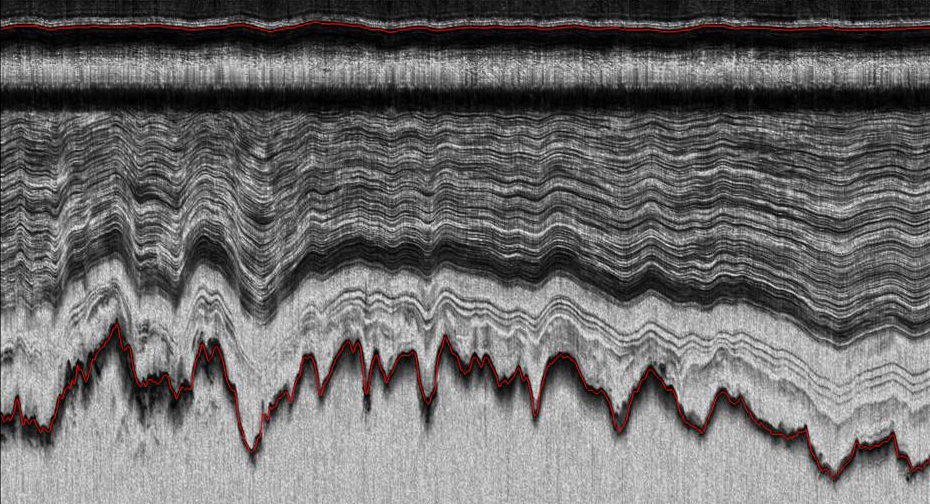
Radar image of the Greenland ice sheet. The ice surface and the ice-bedrock interface are shown in red. This section from North-East Greenland is 160 km long and collected in an area where the ice is frozen to the bedrock and the shape of the internal layers follow the bedrock topography. Courtesy Center for Remote Sensing of Ice Sheets, CReSIS.

The Greenland Ice Sheet is a significant contributor to present sea level rise, even more than Antarctica currently. It is thus important to accurately project the future behavior of the ice sheet, and thus its impact on sea level rise. The projections of have suffered from ad-hoc initialization methods, lack of observational constraints, and lack of rigorous calibration methods.

A well-calibrated model in harmony with the flow history of the Greenland Ice Sheet is likely to be immune to problems such as model drift, and thus provide us with more accurate future predictions. The flow history needs to be teased out of the recently collected ice radar data of the age layers within the ice sheet. This exercise is essentially a PDE-constrained inverse problem, where we look to minimize the model-data misfit subject to constraints such as conservation of mass, momentum and energy expressed in the form of partial differential equations. The problem is ill-posed, and thus a suitable regularization (which in the Bayesian sense is the prior) is also essential.

We leverage the Ice Sheet Model SICOPOLIS to perform this calibration using adjoint based techniques (loosely equivalent to backpropagation in Machine Learning), where the adjoint is derived using the Automatic Differentiation tool Tapenade. Since it is not feasible to get the Hessian, we aim to leverage Quasi-Newton methods for this optimization. Finally, we will also quantify uncertainties using the Bayesian framework, using the Gauss-Newton approximation of the Hessian, and taking advantage of the fact that the Hessian action in the parameter space can be computed without ever fully storing or computing the Hessian directly.